實現非線性修正的前提是需要得到智能渦街流量計流量Q與儀表系數K的關系曲線,再將超出線性度范圍的儀表系數修正到合理的范圍內。文章對三種常用的曲線逼近方法:線性插值法、三次樣條插值法和最小二乘法進行了比較,具體方法如下 對于智能渦街流量計來說,由于在小流量時普遍存在著K-Q之間的非線性,即使在線性度范圍內,K也很難保證為常數,這給用數學公式描述兩者的之間關系帶來很大困難,插值(或曲線擬和)方法能很好地解決這一問題。根據速度式流量計檢定規程,可以將檢定點作為插值函數的結點(或曲線擬和的觀測點),即各檢定流量點Qi(i=0,1,⋯,n),各結點(或觀測點)對應的函數值為Ki(i=0,1,⋯,n),即各流量點對應的儀表系數。根據這些列表函數,可以利用插值多項式(或擬和多項式)對其他流量點的儀表系數進行逼近。
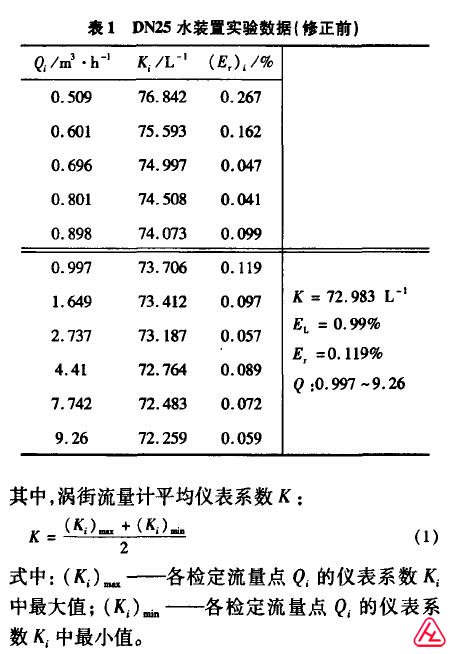
選擇流量點0.509、0.997、1.649、2.737、4.41、7.742和9.26 rn3/h作為插值函數的結點進行分段插值,采用線性插值法和三次樣條插值法,同時作為最小二乘法的觀測點進行曲線擬和,對剩余流量點0.601、0.696、0.801和0.898 m3/h的儀表系數進行逼近,最后與實驗結果進行比較得到表2與圖l一圖3。
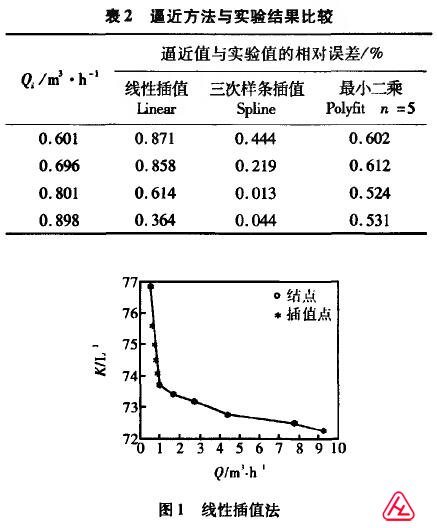 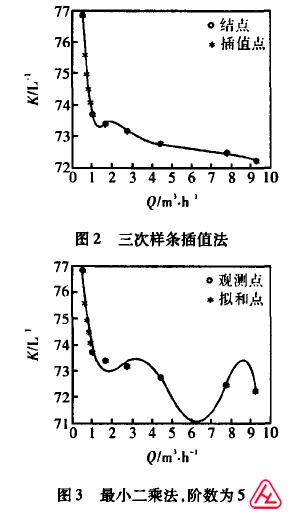 通過比較,利用三次樣條插值法得到的逼近點誤差相對較小,且能夠很好反映曲線變化趨勢。所以在利用CPLD進行儀表系數非線性修正時,選擇用三次樣條插值法對各流量點的儀表系數進行逼近。 |
智能渦街流量計修正算法比較
時間:2017-09-20 21:37來源:專業文章 作者:智能渦街流量計 點擊:次
實現非線性修正的前提是需要得到智能渦街流量計流量Q與儀表系數K的關系曲線,再將超出線性度范圍的儀表系數修正到合理的范圍內。文章對三種常用的曲線逼近方法:線性插值法、三次樣條插值法和最小二乘法進行了比較,具體方法如下 對于智能渦街流量計來說,由
------分隔線----------------------------
- 上一篇:四氟型渦街流量計介紹
- 下一篇:智能渦輪流量計壓力信號采集模塊